Linear regression in sqlite

Linear regression is a very simple, powerful tool to predict the future. Especially when directly implemented in sqlite. This article is based on data from my PV system. From which I want to predict three things:

• at what time the PV system starts to generate power,
• when the most power is expected to be generated and
• when the PV system stops again.

These predictions can be useful to plan when to turn on home appliances, and thus use more of the self produced energy and rely less on the grid. I cannot base the prediction on historical data, and due to clouds and shade of nearby trees I cannot derive the prediction from the time the sun rises and sets. So the prediction will be based on the last 30 days of data.

Approach

The linear regression is implemented in sqlite, because, that's where the data is. The python code handling the result can remain very simple, which is a nice side effect. To do this we start simple, and wrap each result in an outer query, which runs over the previous result. So let's implement a linear regression on time series data in sqlite!

Source Data

The source data looks like this:

select TimeStamp,ETotal from spotdata limit 10 offset 2000;

TimeStamp	ETotal
1598427906	16329548
1598427926	16329548
1598427946	16329549
1598427986	16329549
1598428006	16329550
1598428026	16329550

A timestamp and an ever increasing counter.

Relying heavy on sql windows functions we transform this into a input for our regression. This table will be referred to as input in the rest to this article.

day	start	max	end	count
1	28970	51420	51441	1
2	26179	33600	52499	1
... data omitted for readability ...
29	31660	34860	53043	1
30	31121	68580	68629	1

Here we see for the last 30 days at which time on that day the energy production:

• started,
• reached it's maximum and
• stopped.

The last 'count' column only exists as an artefact and will be omitted. The time is counted in seconds from the start of the day at midnight.

Linear Regression

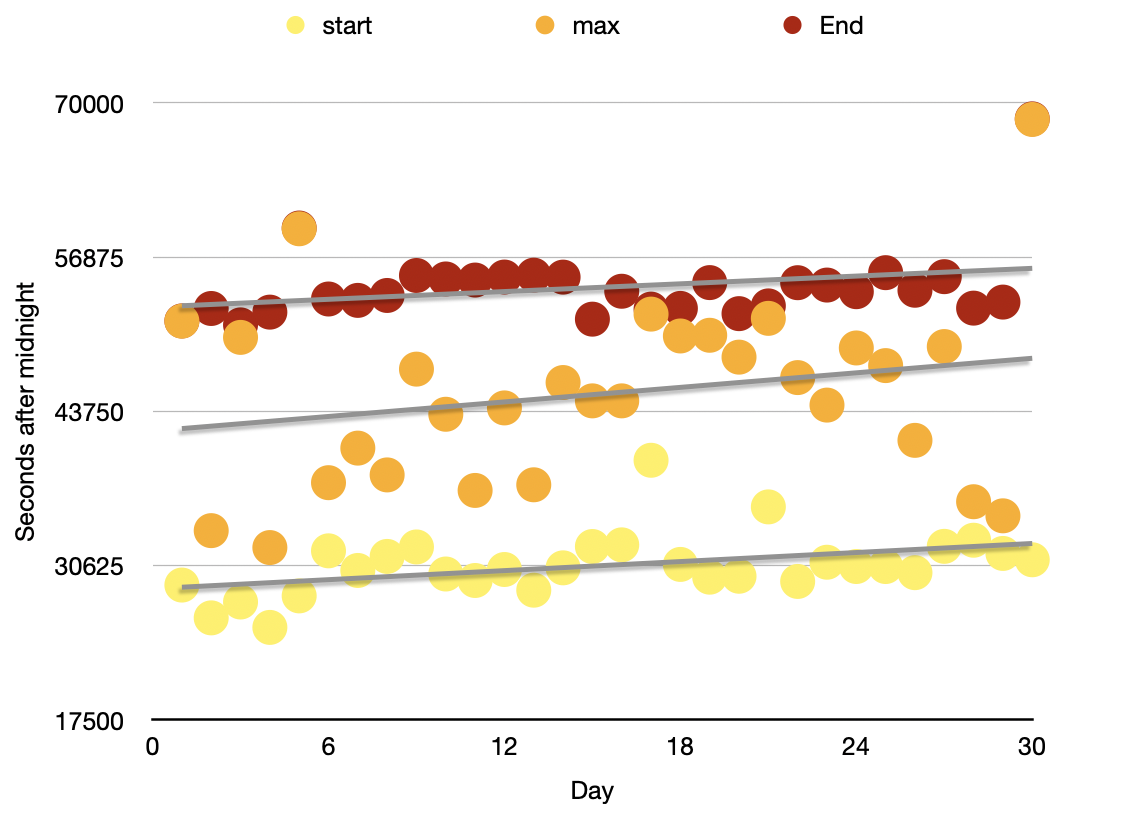
This image shows what I want to achieve. The linear regression for each series is overlaid in gray. This way I can extend the regression line and predict the values for the current day and tomorrow.

As you can see, a linear regression is the best fitting line for the series. Best fitting means the total distance of all point to the line is minimized.

Definition

The equation can be found in any statistical analytics text book:

y=m∙x+b

Where m is called the slope which determines the direction of the line and b is called the intercept which defines the distance of the line from 0.

m is calculated:

m=∑(x_i - ẍ)(y_i - ÿ) / ∑(x_i - ẍ)²

and b is calculated using m :

b=max y - max x ∙ m

Where ẍ and ÿ are the averages of x and y.

Slope

First we calculate (x_i - ẍ)(y_i - ÿ). We do this by using the window function for avg. This adds the average to the each row in the result set:

select
	day, avg(day) over () as day_bar,
	start, avg(start) over () as start_bar,
	max, avg(max) over () as max_bar,
	end, avg(end) over () as end_bar
from input

day	day_bar	start	start_bar	max	max_bar	end	end_bar
1	15.5	28970	30647.0	51420	45272.0	51441	54322.8
2	15.5	26179	30647.0	33600	45272.0	52499	54322.8
3	15.5	27529	30647.0	50040	45272.0	51102	54322.8
...	...	...	...	...	...	...	...

Next we add the summaries as follows to calculate the slope:

select
	sum((day - day_bar) * (start - start_bar)) / 
		sum((day - day_bar) * (day - day_bar)) as start_slope,
	sum((day - day_bar) * (max - max_bar)) / 
		sum((day - day_bar) * (day - day_bar)) as max_slope,
	sum((day - day_bar) * (end - end_bar)) / 
		sum((day - day_bar) * (day - day_bar)) as end_slope
from (
	<previous query omitted for readability>
)

start_slope	max_slope	end_slope
128.292324805339	206.255839822024	109.764627363737

Intercept

With the slope we can calculate the intercept.

b=max y - max x ∙ m

As you can see in the equation, we also need the max in the previous query.

select
	start_slope,
	start_bar_max - day_bar_max * start_slope as start_intercept,
	max_slope,
	max_bar_max - day_bar_max * max_slope as max_intercept,
	end_slope,
	end_bar_max - day_bar_max * end_slope as end_intercept
from (
select	
	sum((day - day_bar) * (start - start_bar)) / 
		sum((day - day_bar) * (day - day_bar)) as start_slope,
	sum((day - day_bar) * (max - max_bar)) / 
		sum((day - day_bar) * (day - day_bar)) as max_slope,
	sum((day - day_bar) * (end - end_bar)) / 
		sum((day - day_bar) * (day - day_bar)) as end_slope,
	max(day_bar) as day_bar_max,
	max(start_bar) as start_bar_max,
	max(max_bar) as max_bar_max,
	max(end_bar) as end_bar_max
from (
	<previous query omitted for readability>

start_slope	start_intercept	max_slope	max_intercept	end_slope	end_intercept
128.292324805339	28658.4689655172	206.255839822024	42075.0344827586	109.764627363737	52621.4482758621

Predict the future!

With the slope and intercept for each series it's trivial to calculate the prediction for today or tomorrow. The example uses 30 days history, so tomorrow is the 31^st day.

We add the following outer query to the query from above:

select 	
	time(start_slope * 31 + start_intercept, 'unixepoch', 'localtime') 
	as start_time,
	time(max_slope * 31 + max_intercept, 'unixepoch', 'localtime') 
	as max_time,
	time(end_slope * 31 + end_intercept, 'unixepoch', 'localtime') 
	as end_time
from (
	<previous query omitted for readability>
)

And here is our prediction:

start_time	max_time	end_time
09:03:55	13:27:48	15:33:44

The result of an linear integration, over time series data, right in sqlite! The result is ready to be used in any control or visualization.

To conclude, the complete query:

select 
	time(start_slope * 31 + start_intercept, 'unixepoch', 'localtime') as start_time,
	time(max_slope * 31 + max_intercept, 'unixepoch', 'localtime') as max_time,
	time(end_slope * 31 + end_intercept, 'unixepoch', 'localtime') as end_time
from (

select	
	start_slope,
	start_bar_max - day_bar_max * start_slope as start_intercept,
	max_slope,
	max_bar_max - day_bar_max * max_slope as max_intercept,
	end_slope,
	end_bar_max - day_bar_max * end_slope as end_intercept
from(

select	
	sum((day - day_bar) * (start - start_bar)) / sum((day - day_bar) * (day - day_bar)) as start_slope,
	sum((day - day_bar) * (max - max_bar)) / sum((day - day_bar) * (day - day_bar)) as max_slope,
	sum((day - day_bar) * (end - end_bar)) / sum((day - day_bar) * (day - day_bar)) as end_slope,
	max(day_bar) as day_bar_max,
	max(start_bar) as start_bar_max,
	max(max_bar) as max_bar_max,
	max(end_bar) as end_bar_max
from (

select	
	day, avg(day) over () as day_bar,
	start, avg(start) over () as start_bar,
	max, avg(max) over () as max_bar,
	end, avg(end) over () as end_bar
from input
)
)
)